variables aléatoires

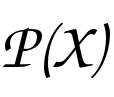variables aléatoires

définitions

On nomme Variable Aléatoire sur <math|f=\Omega> toute application de <math|f=\Omega> dans <math|f=\mathbb{R}>

<math|f= VA (\Omega ) : \Omega \longrightarrow\mathbb{R}>

La loi de probabilité (ldp) d’une variable aléatoire <math|f=X> est l’application <math|f=f_{X}> de <math|f=X(\Omega )> dans <math|f=\mathbb{R}> associant à tout x de <math|f=X(\Omega )> le nombre <math|f=f_X(x)=P(X=x)>

<math|f=\begin{array}{lrccl} ldp : & f_X : &X(\Omega ) &\mapsto &\mathbb{R} \\ & & x &\longrightarrow &P(X=x) \end{array} >

La fonction de répartition de <math|f=X> est l’application <math|f=F_X> de <math|f=\mathbb{R}> dans <math|f=\mathbb{R}> associant à tout x le nombre <math|f=F_X(x)=P(X\leq x)>

<math|f=\begin{array}{lrccl} fdr : & F_X : &\mathbb{R} &\longrightarrow&\mathbb{R} \\ & & x &\mapsto &P(X\leq x) \end{array} >

lois de probabilité discrète

Loi de Poisson : loi qui décrit le comportement du nombre d’évènements se produisant dans un laps de temps fixé, si ces évènements se produisent avec une fréquence moyenne connue et indépendamment du temps écoulé depuis l’évènement précédent.

Loi uniforme : équiprobabilité de chaque valeur.

Loi de bernouilli : <math|f= P(X=1)=p ; P(X=0)=1-p>.
Une épreuve de bernouilli est une expérience aléatoire qui a deux issues possibles, gagné ( resp. perdu ), <math|f=G> ou {1} (resp <math|f=P> ou {0}), <math|f=G=\bar{P}>. Dans une épreuve de Bernoulli de paramètre p, la probabilité de « gagné » est <math|f=p(G)=p>.

Loi de bernouilli : l’univers <math|f=\Omega> contient un nombre fini d’objets. L’univers contient N <math|f=(=card(\Omega))> objets séparés en deux groupes G et P : <math|f=\Omega = G + P>. La probabilité de gagner est <math|f=p(G)=\frac{card(G)}{card(\Omega)}>

Loi binomiale : répéter n fois, de façon indépendante, une épreuve de Bernoulli de paramètre p

Loi binomiale : piocher n fois dans un groupe contenant une proportion p d’objets gagnés. Donc avec remise.

Loi hypergéométrique : On tire simultanément n boules dans une urne contenant pA boules gagnantes et qA boules perdantes (avec q = 1 - p, soit un nombre total de boules valant pA + qA = A). On compte alors le nombre de boules gagnantes extraites et on appelle X la variable aléatoire donnant ce nombre.

Loi géométrique : le temps d’attente de la première réussite <math|f=E=\{000000001\} ; p(n)=(1-p)^{n-1} * p >
Tous les couples ont des enfants jusqu’à obtenir un garcon

lois de probabilité continue

Loi uniforme : tous les intervalles de même longueur inclus dans le support de la loi ont la même probabilité.

Loi exponentielle : la probabilité que le phénomène dure au moins s + t heures sachant qu’il a déjà duré t heures sera la même que la probabilité de durer s heures à partir de sa mise en fonction initiale. <math|f=\bigvee(s,t)\in\mathbb{R}^{+2} , P(X \gt s+t \mid X\gt t ) = P( X \gt s )>

Loi normale : loi de Gauss

<math|f=\begin{array}{llcll} \\ \\ loi\ de\ poisson & & P_{\lambda\gt 0}(X = k )=\frac{\lambda^k}{k!}e^{-\lambda} & E(X) = \lambda & V(X)=\lambda\\ loi\ uniforme & U([a;b[) & \frac{1}{b-a} sur [a;b] & E(X) = \frac{a+b}{2} & V(X)=\frac{(b-a)^2}{12}\\ loi\ exponentielle & \epsilon (\lambda) & \lambda e^{-\lambda t} ; t \geq 0 & E(X)=\frac{1}{\lambda} & V(X)=\frac{1}{\lambda^2}\\ loi\ normale & N(m,\sigma) & \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-m)^2}{2\sigma^2}} & & \\ loi\ de\ bernouilli & & p ; 1-p ; 0 & E=p & V=pq \\ loi\ binomiale & & C^n_k p^k (1-p)^{n-k} & E=np & V=npq\\ loi\ hypergéométrique & & p(k) = \frac{{pA \choose k}{qA \choose {n-k}}}{{A \choose n}} & E=np & V=npq\frac{A-n}{A-1} \end{array} >

calculs de E et V

Loi binomiale

Soit <math|f=f_{n \in \mathbb{N}} : \mathbb{R}\times\mathbb{R} \longrightarrow \mathbb{R} >, <math|f=(a,b) \longrightarrow (a+b)^n>

<math|f=E=\sum_{k=0}^{k=n} k C^n_k p^k (1-p)^{n-k}> On reconnaît <math|f=p \partial_p p^k>

<math|f=\begin{array}{ll} \frac{\partial}{\partial p} f_n(p,b) = \frac{\partial}{\partial p} (p+b)^n = \frac{\partial}{\partial p} \sum_{k=0}^{k=n} C^n_k p^k b^{n-k} \\ \Rightarrow n(p+b)^{n-1} = \sum_{k=1}^{k=n} C^n_k k p^{k-1} b^{n-k} \\ \Rightarrow \frac{\partial f_n}{\partial p} (p,1-p) = n \times 1= \frac{E}{p}\\ d'ou\ E = n \times p \end{array}>

<math|f=V=\sum_{k=0}^{k=n} (k-\bar{k})^2 C^n_k p^k (1-p)^{n-k} = \bar{(k^2)}-(\bar{k})^2> On reconnaît <math|f=p \partial_p k p^k> : <math|f=k^2 p^k \approx \partial_{p^2}(p^k)>

<math|f=\begin{array}{ll} \frac{\partial^2}{\partial p^2} f_n(p,b) = \frac{\partial}{\partial p} ( n(p+b)^{n-1} ) = \frac{1}{p} \frac{\partial}{\partial p} \sum_{k=1}^{k=n} C^n_k k p^k b^{n-k} - \frac{1}{p^2} \sum_{k=1}^{k=n} C^n_k k p^k b^{n-k}\\ \Rightarrow n(n-1)(p+b)^{n-2} = \frac{1}{p^2} \sum_{k=1}^{k=n} C^n_k k^2 p^k b^{n-k} - \frac{1}{p^2} \sum_{k=1}^{k=n} C^n_k k p^k b^{n-k}\\ \Rightarrow \frac{\partial^2 f_n}{\partial p^2} (p,1-p) = n(n-1) = \frac{1}{p^2} \bar{(k^2)} - \frac{1}{p^2} E \\ \Rightarrow V = ( p^2 n(n-1) + np ) - (np)^2 = np - n p^2 = np(1-p) \end{array}>

Approximation de la loi Binomiale par la loi de Poisson

<math|f=C^n_k p^k (1-p)^{n-k} = \frac{\Pi_{i=0}^{i=k-1} n(1-\frac{i}{n}) }{k!} p^k (1-p)^{n-k} = \frac{(np)^k}{k!} (1-p)^{n-k} \Pi_{i=0}^{i=k-1} (1-\frac{i}{n}) >

<math|f== \frac{\lambda^k}{k!} (1-\frac{\lambda}{n})^n (1-\frac{\lambda}{n})^{-k} \Pi_{i=0}^{i=k-1} (1-\frac{i}{n}) >

<math|f=\Delta = \frac{\mid (1-\frac{\lambda}{n})^n - e^{-\lambda}\mid }{e^{-\lambda}} > pour :
<math|f=\begin{array}{lll} & \Delta \le 1\% & \Delta \le 10\% \\ \lambda =0.1 & n \ge 1 & n \ge 1 \\ \lambda =0.5 & n\ge 13 & n\ge 2 \\ \lambda =1.0 & n\ge 51 & n\ge 6 \\ \lambda =3.0 & n\ge 450 & n\ge 45 \\ \lambda =10.0 & n\ge 4982 & n\ge 482 \end{array}>

<math|f=\Delta = \frac{\mid (1-\frac{\lambda}{n})^n - e^{-\lambda}\mid }{e^{-\lambda}} > pour :
<math|f=\begin{array}{lll} & \Delta \le 1\% & \Delta \le 10\% \\ \lambda =0.1 & n \ge 1 ( p\le 0.1 )& n \ge 1 ( p\le 0.1 ) \\ \lambda =0.5 & n\ge 13 ( p\le 0.04 )& n\ge 2 ( p\le 0.25 ) \\ \lambda =1.0 & n\ge 51 ( p\le 0.02 )& n\ge 6 ( p\le 0.16 ) \\ \lambda =3.0 & n\ge 450 ( p\le 0.007 )& n\ge 45 ( p\le 0.07 )\\ \lambda =10.0 & n\ge 4982 ( p\le 0.002 )& n\ge 482 ( p\le 0.02 ) \end{array}>

<math|f=\begin{array}{lllllll} & C^n_k p^k (1-p)^{n-k} & l^^k/k! e-l \\ \lambda=1.0;n=51.0;k=10.0 & \end{array}>

ca marche jusqu’à <math|f=k^2 = n/2>

<math|f=\begin{array}{lllllll} & & (1-\frac{\lambda}{n})^{-k} & \Pi_{i=0}^{i=k-1} (1-\frac{i}{n}) & (1-\frac{\lambda}{n})^n & produit & e^{-\lambda}\\ \lambda =0.1;n = 10 & k=5 & 1.05&0.3&0.9&0.29&0.9\\ \lambda =0.5;n = 13 & k=5 & 1.22&0.41&0.6&0.3&0.6\\ \lambda =0.5;n = 13 & k=3 & 1.12& 0.78 &0.6&0.52&0.61\\ \lambda =1.0;n = 51 & k=10 & 1.22 & 0.39 & 0.36 & 0.17& 0.37\\ \lambda =20.0;n = 1000 & k=50 &2.75 & 0.29& 1.68e-09& 1.33e-09 & 2.06e-09\\ \lambda =2.0;n = 1000 & k=50 &1.11&0.29&0.14&0.043&0.14\\ \lambda=2.0; n=1000.0&k=7.0& 1.01& 0.98& 0.14& 0.13& 0.14\\ \lambda=1.0;n=51.0 & k=2.0& 1.04&0.98&0.36&0.37&0.37 \end{array}>